Where to Draw Phase Plane Plot

phaseR: An R package for stage aeroplane analysis of 1 and two-dimensional autonomous ODE systems [1]. The phaseR package uses stability analysis to classify equilibrium points.

Fixed Points and Phase Portraits

Equilibrium points and stability. Equilibrium points of an autonomous ODE are defined at $x^*=0$ such that $f(x^*)=0$. Why exercise we desire to find the equilibrium points? First at a point $x^*$ such that $f(x^*)=0$, the system, if unperturbed, will remain at $x^*$. Hence, these points determine the long-term behavior of a differential equation.

Phase portrait: A phase portrait is divers every bit the geometrical representation of the trajectories of the dynamical system in the stage airplane of the system equation. Every prepare of the initial condition is represented by a different bend or point in the phase airplane.

Linearization

Fixed Points $\mathbf{(10^{\star}, y^{\star})}$: occur for $\mathrm{\dot x = 0}$ and $\mathrm{\dot y = 0}$
Substitute $\mathrm{\dot ten}$ and $\mathrm{\dot y}$ into the Jacobian Matrix

\[ \Large \mathbf{A} = \begin{bmatrix} \mathrm{\frac{\partial{\dot x}}{\fractional x}} & \mathrm{\frac{\partial \dot ten}{\partial y}} \\ \mathrm{\frac{\fractional \dot y}{\partial 10}} & \mathrm{\frac{\partial \dot y}{\partial y}} \end{bmatrix} \]

Evaluate matrix $\mathbf{A}$ at whatsoever fixed signal $\mathbf(x^{\star}, y^{\star})$
The Eigen value $\mathbf{\lambda}$ for the fixed point is calculated with the characteristic equation $\mathrm{det}\mathbf{(A-\lambda I)}=0$.

\[ \begin{align} \large \mathbf{A}_{\minor\mathrm{(ten^{\star}, y^{\star})}} \mathbf{-} \begin{bmatrix} \lambda & 0 \\ 0 & \lambda \terminate{bmatrix} &= 0 & \\ \begin{bmatrix} a_1 - \lambda & a_2 \\ a_3 & a_4 -\lambda \end{bmatrix} &= 0 & \\ (a_1 - \lambda) \times (a_4 -\lambda) - (a_2) \times (a_3) &= 0 \end{marshal} \]

The roots of the above equation tin be calculated equally

\[\lambda = \mathrm{\frac{-b \pm \sqrt{b^ii - 4ac}}{2a}}\]

Sketch the Phase Portrait

Types of Stock-still Points

a. Stable Node

The stock-still indicate volition be a stable node if both eigen values $\lambda_{one,2}$ are real numbers with the aforementioned sign: $\lambda_{1,2} > 0$ or $\lambda_{1,two} < 0$.

b. Saddle Node

The fixed indicate volition be a saddle point if ane eigen value $\lambda_1$ is greater than 0, and the other eigen value $\lambda_2$ is less than 0.

c. Center

The origin of the organization will form a center if both eigen values $\lambda_{1,2}$ are pure imaginary.
The fixed betoken will be an outgoing spirals if both eigen values $\lambda_{i,2}$ are circuitous with positive real parts.
The fixed point will be oscillating in nature if the eigen values $\lambda_i$ change from existent to imaginary.

d. Isolated

The origin will exist an isolated fixed indicate if the determinant $\nabla$ comes out to be 0.

e. Unstable Star

The fixed point will be a unstable star if there is only one eigen value $\lambda_1$ for the organization.

Equilibrium points

Example. Find the equilibrium points to the post-obit ODE:

\[\frac{dy}{dt}=4-y^2\]

\[ \begin{marshal} \frac{dy}{dt} &= 4-y^ii = 0 \\ 0 & = (2-y)(ii+y) \\ \Rightarrow& y = -2,2 \end{align} \]

Stability of the equilibrium points

Definition. if for every $\epsilon>0$, there exists $\delta>0$ such that whenever $|y(0)-y_*|<\delta$ then $|y(t)-y_*|<\epsilon$ for all $t$. Hence, a stock-still point is stable if a organisation placed a small-scale distance away from the fixed bespeak continues to remain close to the fixed point. And a fixed point is unstable if a organization placed a minor perturbation away from the stock-still point causes the solution to diverge.

There are 2 methods for determining the stability of a stock-still bespeak: Phase Portrait Analysis or the Taylor Serial Expansion.

Phase Portrait Analysis

Graphical Interpretation. A phase portrait plots the derivative $\dot x$ against the dependent variable $x$. We can find the equilibrium points at locations where $f$ crosses the $\mathcal ten-\text{centrality}$.

We can stand for the flow of $f$ in the phase portrait by placing arrows forth the dependent variable's axis, indicating whether $f$ would be increasing or decreasing. Points where arrows on both side of the equilibrium point towards each other $\rightarrow\;\; \leftarrow$ denotes stability. And points where arrows on both side of the equilibrium betoken away from each other $\leftarrow\;\; \rightarrow$ denotes instability.

In the following, we plot the phase portrait for $\frac{dy}{dt}=4-y^2$. The trajectories plotted shows that solutions converge towards $y=two$, but away from $y=-2$. Hence, the equilibrium point $y^*=2$ is stable and the equilibrium point $y^*=-2$ is unstable.

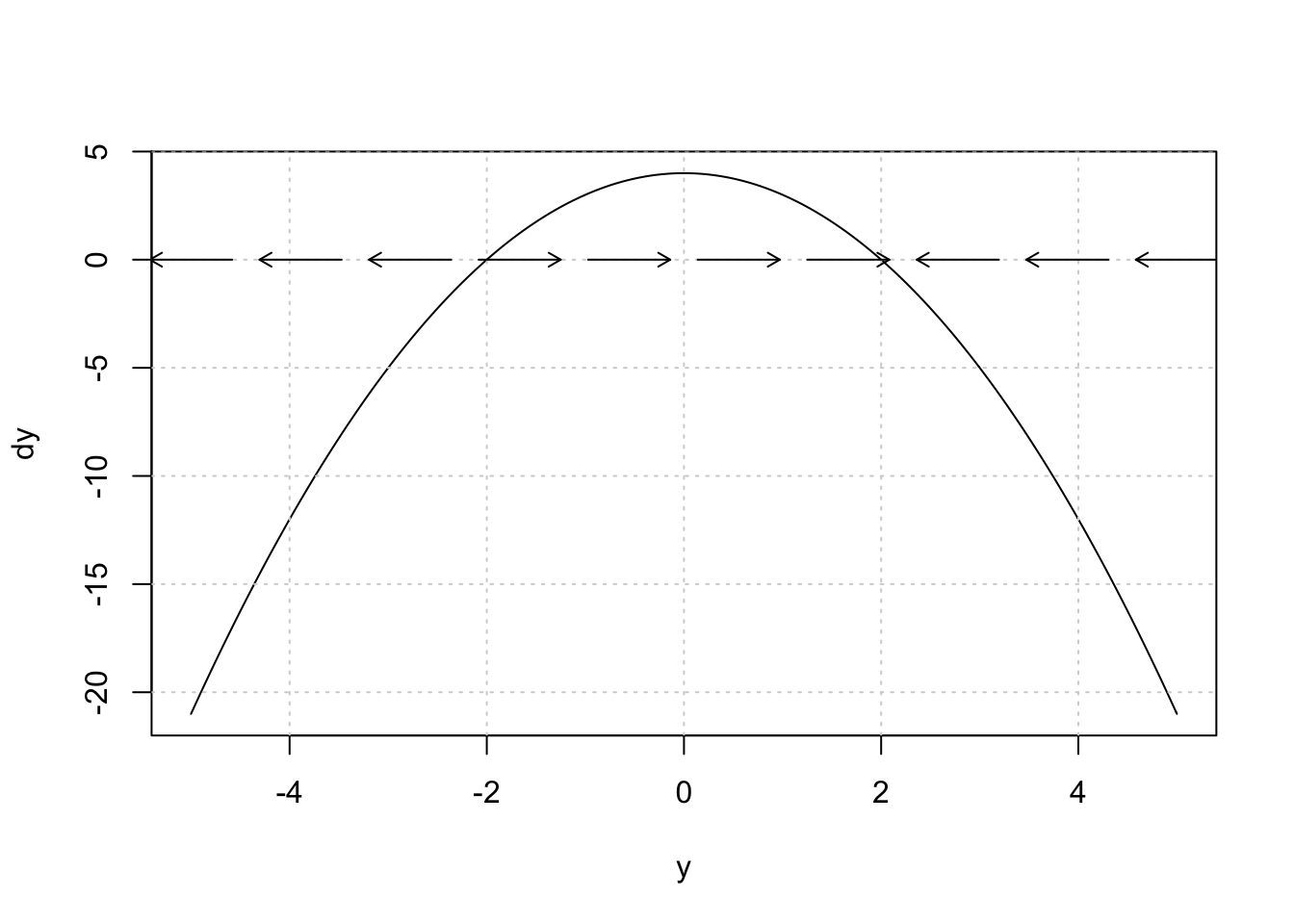
$Figure 1: Phase Portrait for $\frac{dy}{dt}=4-y^2$. The trajectories plotted shows that solutions converge towards $y=2$, but away from $y=-2$.$

Figure 1: Phase Portrait for $\frac{dy}{dt}=4-y^2$. The trajectories plotted shows that solutions converge towards $y=2$, only away from $y=-two$.

Uniqueness Theorem. The higher up method assumes $f$ to be continuous and differentiable. Hence, these conditions guarantee only unique solutions to the autonomous differential equation. Therefore, the solution curves cannot bear upon, expect when they converge at equilibrium points.

Taylor Series Expansion

The second method for performing stability analyses utilizes the Taylor Series expansion of $f$.

Assumptions: Suppose we are a modest altitude $\delta(0)$ away from fixed signal $y_*$. Then $y(0)=y_*+\delta(0)$ and $y(t)=y_*+\delta(t)$. So, the Taylor Series of $f$ tin be written every bit the following, such that the $y^*$ input represents the point where we perform stability analysis:

\[f(y^*+\delta)=f(y^*)+\delta\frac{\partial f}{\partial y}(y^*)+o(\delta)\]

Example i. I-Dimesnional ODE

Consider the one-dimensional autonomous ODE: \[\frac{dy}{dt}=y(1-y)(2-y)\]

Flow Field

The post-obit plots the menses field and diverse trajectories, calculation horizontal lines at equilibrium points:

Figure 2: The flow field and various trajectories, adding horizontal lines at equilibrium points.

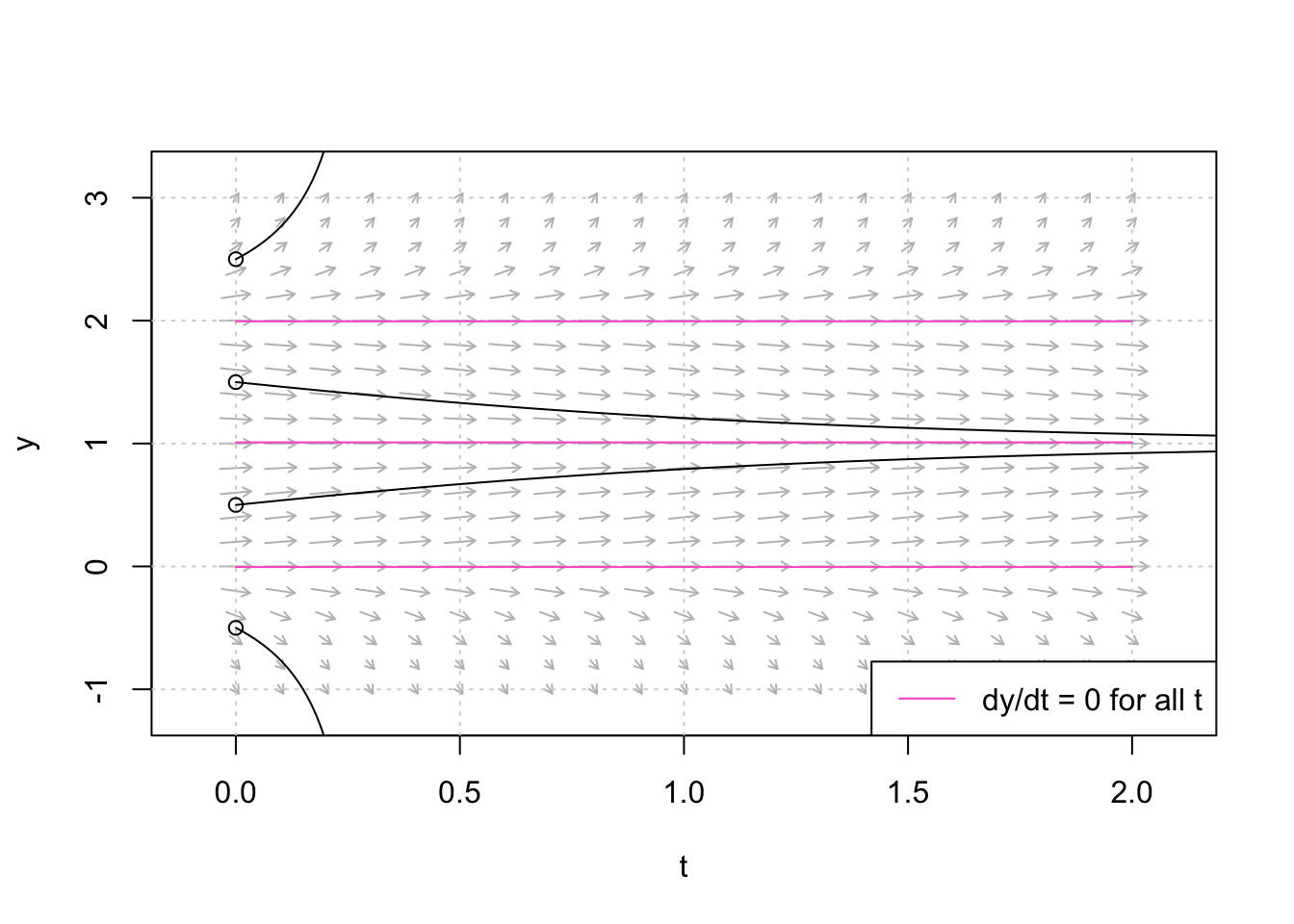
Effigy 2: The menses field and various trajectories, adding horizontal lines at equilibrium points.

Fixed Points

The horizontal lines on the graph betoken that three equilibrium points take been identified at $y^*=0,1,2$. If we set $\lid y=0,$ we tin analytically solve for the iii equilibrium points:

\[ \begin{marshal} y^* (one-y^* )(2-y^* ) &= 0 \\ y^* &= 0, ane, 2 \end{align} \]

Stability of Fixed Points

Method 1. Phase Portrait

Plotting the phase portrait, we notice that $y^*=0$ and $y^*=2$ are unstable; and $y^*=1$ is stable

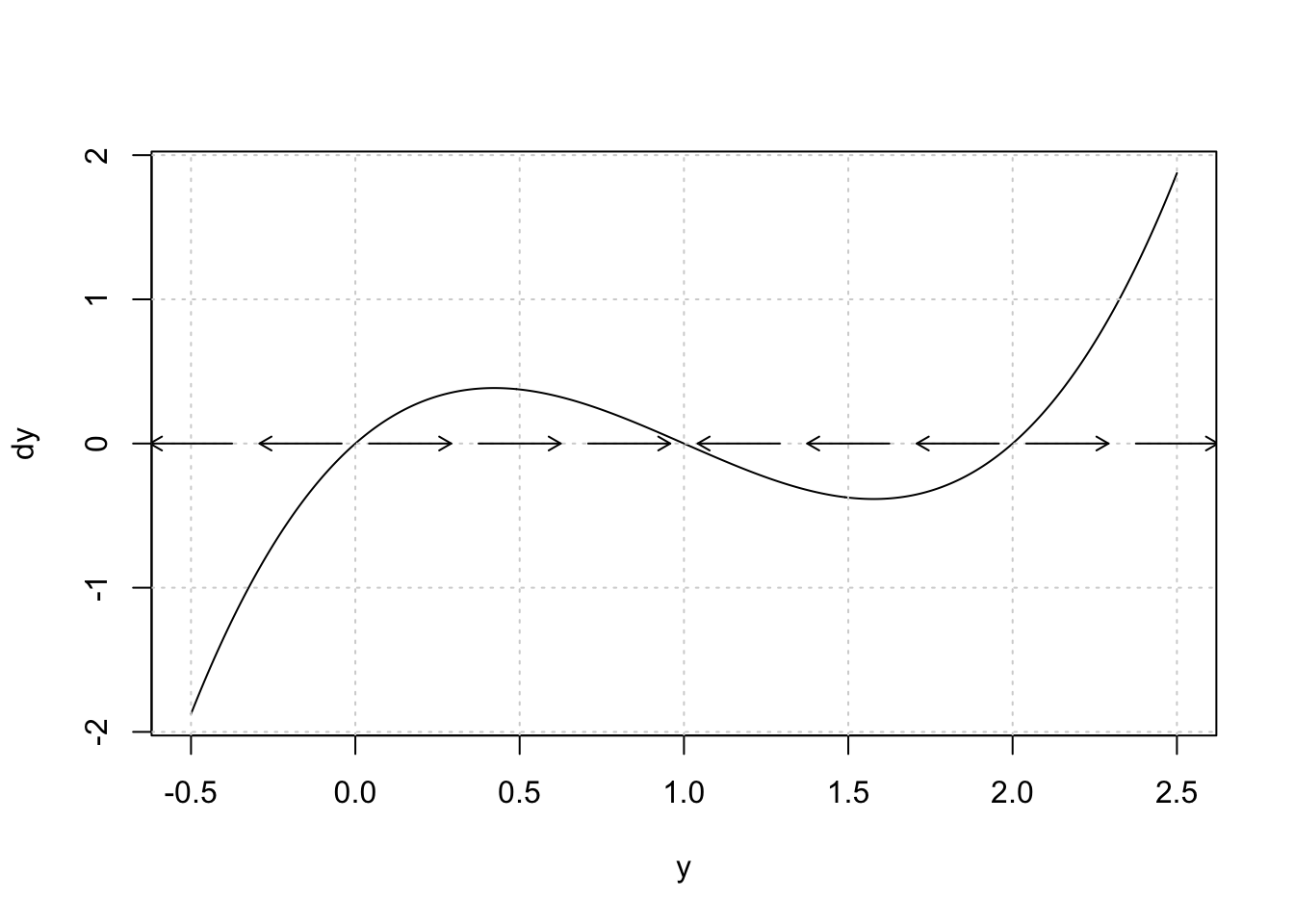
Figure 3: The flow field and various trajectories, adding horizontal lines at equilibrium points.

Figure iii: The flow field and various trajectories, adding horizontal lines at equilibrium points.

Method 2. Taylor Series Approach

\[ \brainstorm{align} \frac{dy}{dt}&=y (one-y )(2-y ) \\ &= y^3-4y^2+2y \end{marshal} \]

Using the Taylor Series approach we take:

\[ \brainstorm{align} \frac{d}{dy}\left.\left(\frac{dy}{dt}\right)\right|_{y=y^*} &= 3y^{*^2} - 6y^* + 2 = \brainstorm{cases} two, & \ y^*=0,\\ -1 ,& \ y^*=i,\\ 2, & \ y^*=ii. \end{cases} \finish{align} \]

We draw the same conclusion as from the stage portrait. We can ostend the Taylor analysis using stability() to bank check the stability of each equilibrium bespeak:

Hence nosotros attain conclusion as above that $y^*=two$ is stable, and $y^*=-two$ is unstable. Therefore, if $y(0)>2$ or $0<y(0)<2$, then the solution will somewhen arroyo $y=2$. However, if $y(0)<0$, $y\rightarrow-\infty$ as $t\rightarrow\infty$.

Example ii. Two-Dimensional ODE

Consider the Lotka-Volterra model, a unproblematic two species competition model, used in ecology, given by the following:

\[\frac{dx}{dt} = x-xy, \ \frac{dy}{dt} = xy-y\]

a. Plot the velocity field with several trajectories:

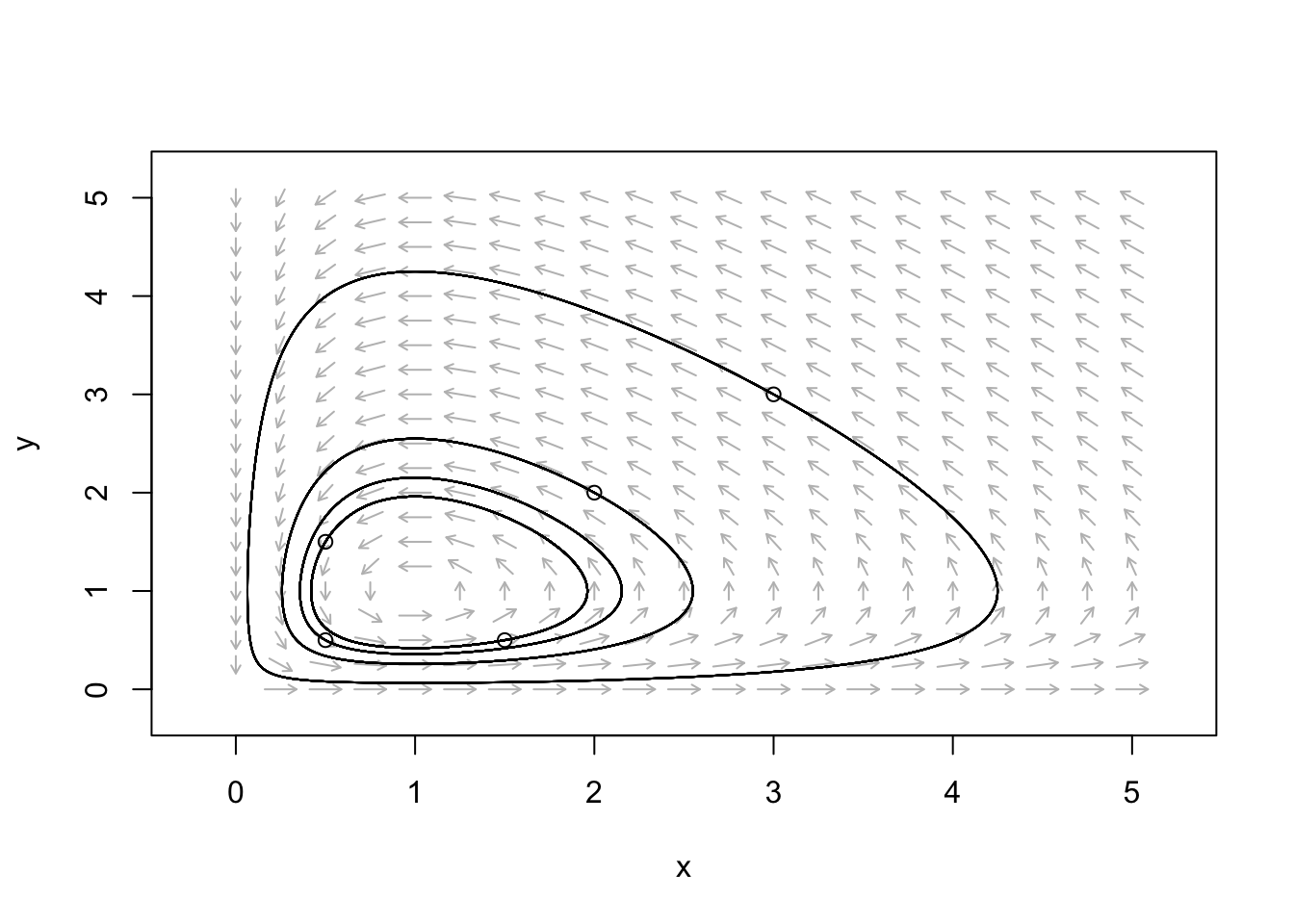
$Figure 4: Plot of the velocity field with several trajectories for $\frac{dx}{dt} = x-xy, \frac{dy}{dt} = xy-y$.$

Figure four: Plot of the velocity field with several trajectories for $\frac{dx}{dt} = x-xy, \frac{dy}{dt} = xy-y$.

Nullclines

Here, $x$-nullclines are divers where $f(x,y)=0$, while the $y$-nullclines are divers where $thousand(x,y)=0$. Thus, the $x$- and $y$-nullclines define the locations where $x$ and $y$ do not change with time $t$. When plotting a vector field, it is a skillful idea to plot the nullclines outset, considering the line segments/vectors along the nullclines move parallel to the $x$- and $y$-axes.

b. Summate and Sketch the Nullclines:

\[ \begin{align} \mathbf{\dot x = 0} \\ & \mathrm{x-xy = 0} \ \Longrightarrow \ 10(1-y) = 0 \\ & \Rightarrow \mathbf{10=0} \text{ or } \mathbf{y=1},\\ \mathbf{\dot y = 0}\\ & \mathrm{xy-y = 0} \Rightarrow y(10-1) = 0 \\ & \Rightarrow \mathbf{ten=ane} \text{ or } \mathbf{y=0} \cease{align} \]

Hence, the stock-still points come up out to exist $\mathrm{(0, 0)}$ and $\mathrm{(1, 1)}$.

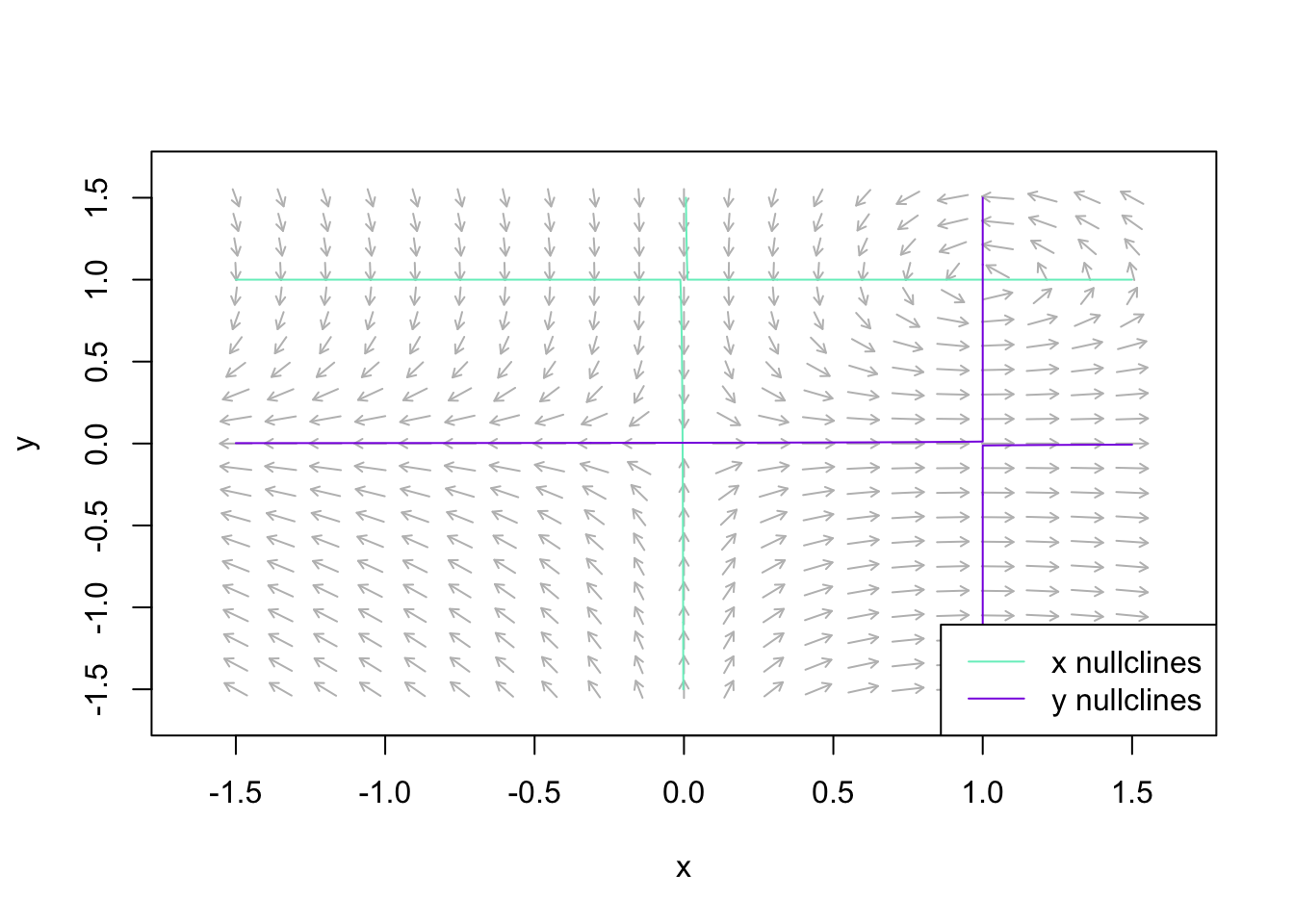
$Figure 5: Sketch of the nullclines for the system of equations $\frac{dx}{dt} = x-xy, \frac{dy}{dt} = xy-y$.$

Figure 5: Sketch of the nullclines for the arrangement of equations $\frac{dx}{dt} = x-xy, \frac{dy}{dt} = xy-y$.

Equilibrium points and stability

Equilibrium points divers as the Fixed points are at $(x_*,y_*)$ where:

\[ f(ten^*,y^*)=1000(x^*,y^*)=0 \]

c. Taking partial derivatives we compute the Jacobian at whatever equilibrium point $(x^∗,y^∗)$:

\[ \begin{align} \mathbf{A} &= \brainstorm{bmatrix} \frac{\partial (x-xy)}{\partial x} & \frac{\fractional (x-xy)}{\fractional y} \\ \frac{\partial (xy-y)}{\fractional x} & \frac{\partial (xy-y)}{\partial y} \end{bmatrix} \\ \\ \mathbf{A}_{(x,y)} &= \begin{pmatrix} \mathrm{1-y} & \mathrm{-10} \\ \mathrm{y} & \mathrm{x-ane} \stop{pmatrix} \stop{align} \]

For the fixed betoken $\mathbf{(0,0)}$

\[ \mathbf{A}_{(0,0)} = \left.\begin{pmatrix} \mathrm{1} & \mathrm{0} \\ \mathrm{0} & \mathrm{-one} \end{pmatrix}\correct|_{(0,0)} \]

So $\text{tr}(J)=T=0$ and $\text{det}(J)=\Delta=-i$; which from our table above makes $(0,0)$ a saddle point.

For the fixed point $\mathbf{(1,1)}$

\[ \mathbf{A}_{(1,1)} = \left. \brainstorm{pmatrix} \mathrm{0} & \mathrm{-i} \\ \mathrm{1} & \mathrm{0} \terminate{pmatrix}\right|_{(ane,i)} \]

Therefore, $\text{tr}(J)=T=0$ and $\text{det}(J)=\Delta=ane$; which from our table above makes $(1,1)$ a centre.

If we look back at our earlier plot, we tin notice trajectories diverging away from $(0,0)$, but traversing effectually $(1,1)$.

d. Plot the Oscillating Nature

Hither we plot $10$ and $y$ trajectories against $t$. For the example of $(x_0,y_0)=(3,4)$ in this case organization this results in the following plot which nosotros tin can view the aquiver nature of $10$ and $y$:

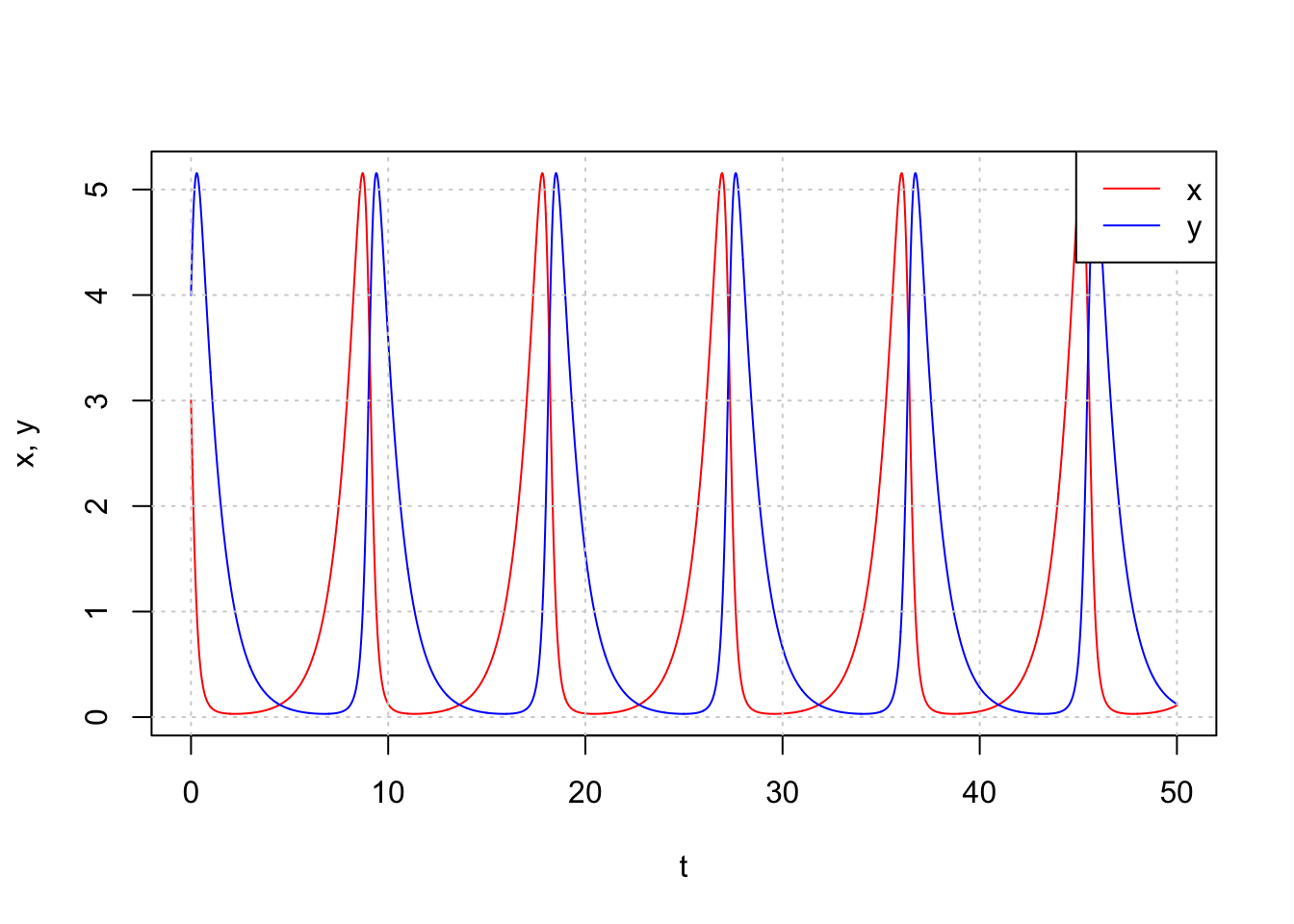
Figure 6: Plot $x$ and $y$ trajectories against $t$. In this example, we can view the oscillating nature of $x$ and $y$.

Effigy 6: Plot $ten$ and $y$ trajectories confronting $t$. In this example, we can view the oscillating nature of $x$ and $y$.

Example three. Wilson-Cowan Model

The Wilson-Cowan Organisation is a coupled, nonlinear, differential equation for the excitatory and inhibitory populations' firing rates of neurons:

\[\tau_e \frac{dE}{dt} = -Eastward + (k_e - r_e E) \, S_e(c_1 E - c_2 I + P)\]

\[\tau_i \frac{dI}{dt} = -I + (k_i - r_i I) \, S_i(c_3 East - c_4 I + Q),\]

In our numerical search of the steady-state points, we study the cases where the derivatives of $E$ and $I$ are zip. Since the system is highly nonlinear, nosotros have to practise it numerically. First, nosotros draw the catamenia field so draw the nullclines of the organisation. The $x$-nullclines are divers past $f(x,y)=0$, and the $y$-nullclines are defined past $g(10, y)=0$. These are the locations where $x$ and $y$ practise non alter with fourth dimension.

Limit Cycles. Non-linear systems tin can exhibit a type of beliefs known every bit a limit cycle. If at that place is only one steady-state solution, and if the steady-country solution is unstable, a limit cycle will occur. In the following, nosotros define the parameters for satisfying conditions 18 and twenty equally $c_1=xvi$, $c_2 = 12$, $c_3=15$, $c_4=three$, $a_e = 1.3$, $\theta_e=4$, $a_i=2$, $\theta_i = iii.vii$, $r_e=i$ and $r_i=one$. We can decide a steady-land solution by the intersection of the nullclines as follows.

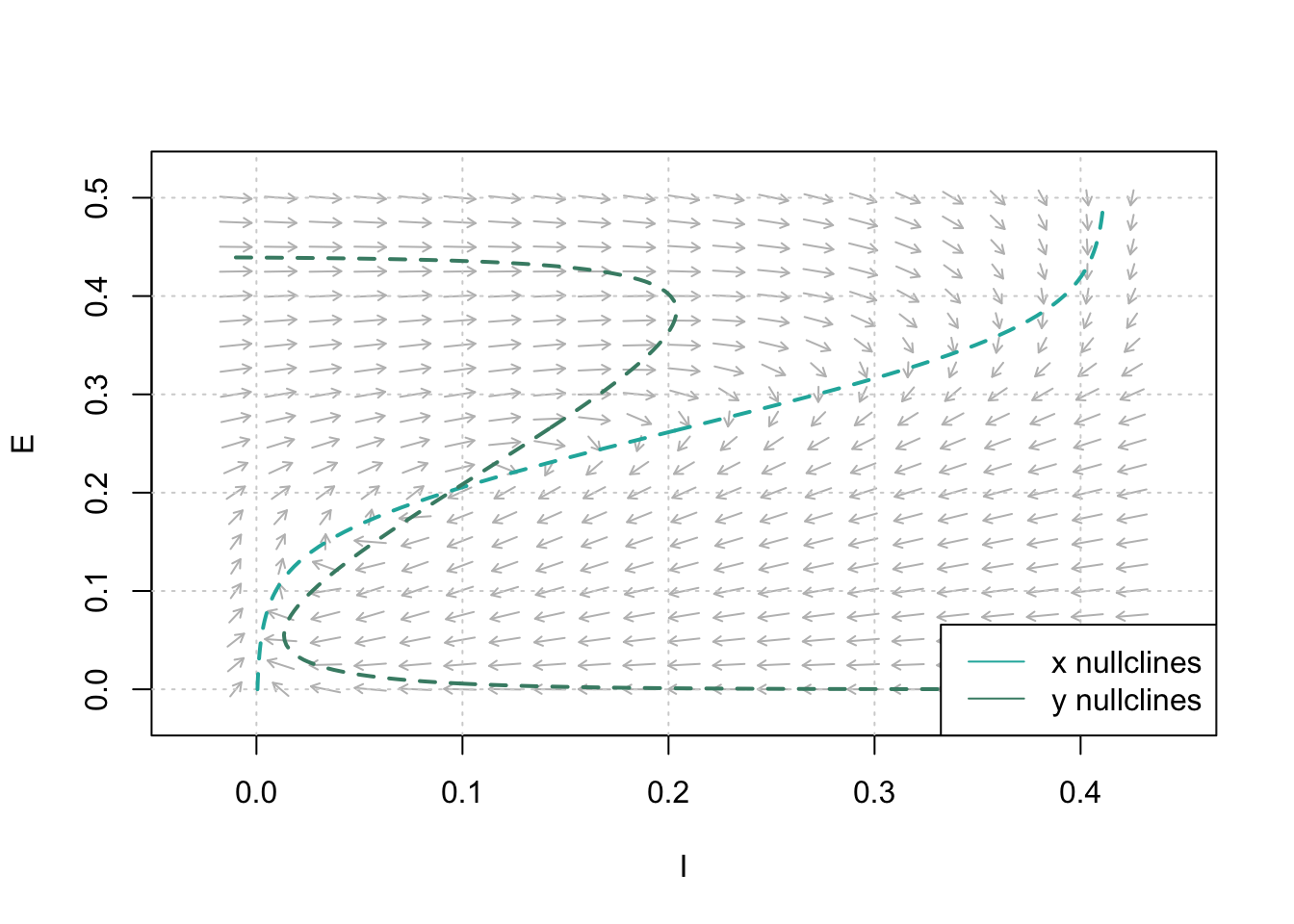
$Figure 7: Phase Plane Analysis. Determine the steady-state solution by the nullclines' intersection. Parameters: $c_1=16$, $c_2 = 12$, $c_3=15$, $c_4=3$, $a_e = 1.3$, $\theta_e=4$, $a_i=2$, $\theta_i = 3.7$, $r_e=1$, $r_i=1$.$

Figure 7: Stage Plane Analysis. Determine the steady-country solution by the nullclines' intersection. Parameters: $c_1=16$, $c_2 = 12$, $c_3=15$, $c_4=3$, $a_e = ane.3$, $\theta_e=iv$, $a_i=2$, $\theta_i = 3.vii$, $r_e=i$, $r_i=1$.

In the phase airplane, the limit cycle is an isolated closed orbit, where "airtight" ways the periodicity of movement, and "isolated" means the limit of motion, where nearby trajectories converge or deviate. Nosotros can alter our initial values of $E_0$ and $I_0$ to obtain dissimilar paths in the phase space.

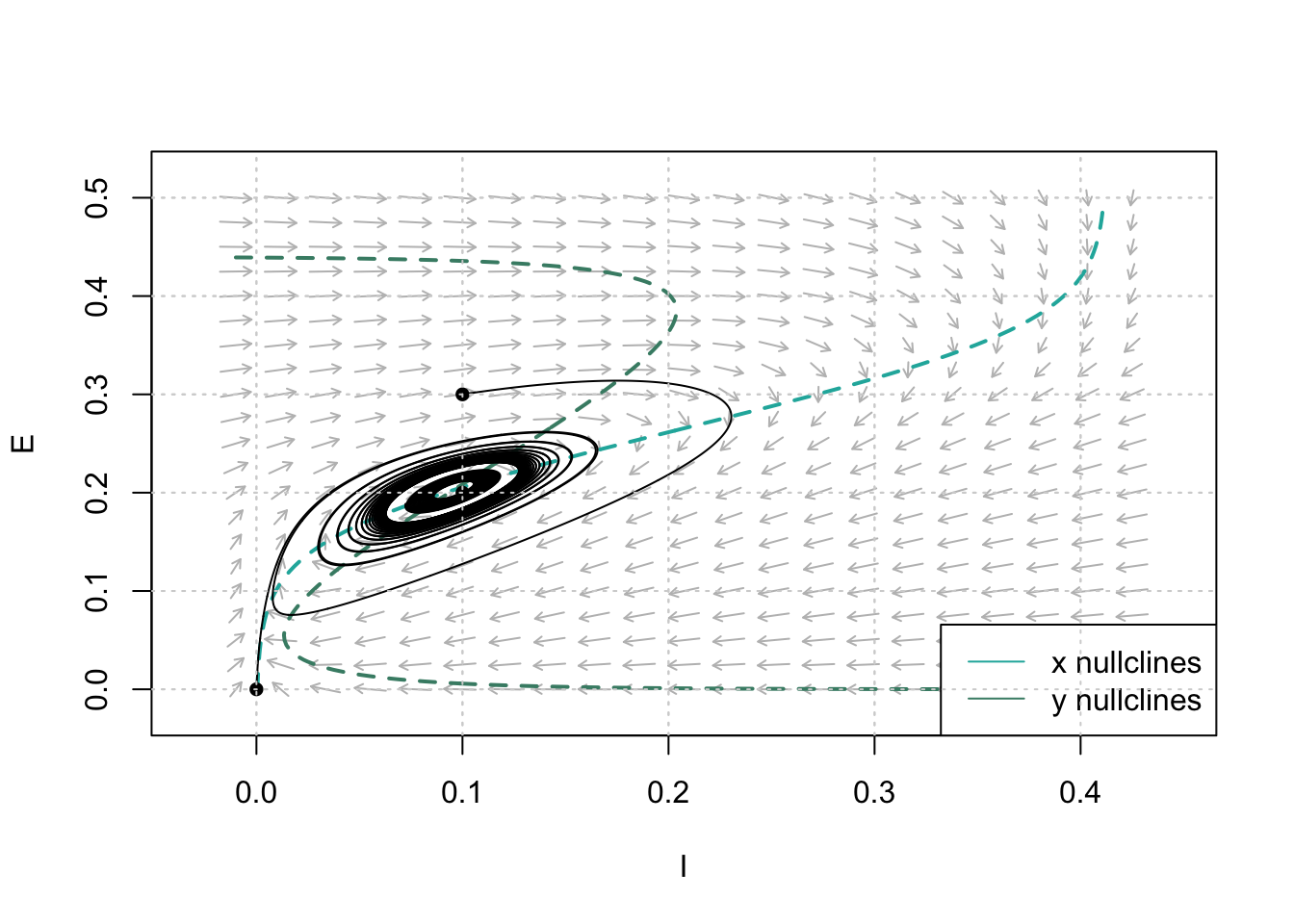
$Figure 8: Phase Plane Analysis showing limit cycle trajectory in response to constant simulation $P=1.25$. Dashed lines are nullclines. Parameters: $c_1=16$, $c_2 = 12$, $c_3=15$, $c_4=3$, $a_e = 1.3$, $\theta_e=4$, $a_i=2$, $\theta_i = 3.7$, $r_e=1$, $r_i=1$.$

Figure eight: Phase Plane Analysis showing limit bicycle trajectory in response to constant simulation $P=i.25$. Dashed lines are nullclines. Parameters: $c_1=xvi$, $c_2 = 12$, $c_3=15$, $c_4=3$, $a_e = 1.iii$, $\theta_e=4$, $a_i=2$, $\theta_i = iii.7$, $r_e=1$, $r_i=one$.

The phase plane analysis illustrates a divisional steady-state solution that is classified as unstable; this is a typical feature of a limit cycle. The solution's aquiver beliefs, shown in Figure ten, follows typical limit cycle beliefs:

Trajectories near the equilibrium point are pushed farther away from the equilibrium.
Trajectories far from the equilibrium point motility closer toward the equilibrium.

Nosotros established the resting state $Eastward=0, I=0$ to be stable in the absence of an outside force. Therefore, the neural population only exhibits limit cycle activity in response to a constant external input (P or Q). All in all, the premise of Theorem 3 is that there is only one steady-state, and it must be near the inflection point for a limit cycle to exist. Therefore, if nosotros report the limit behavior as a function of $P$, where $Q=0$, then it follows that:

At that place is a threshold value of P, and below this threshold, the limit cycle action cannot occur.
There is a higher value of P, and above this leap, the organisation's limit cycle action will end.
Within the range defined in a higher place, both the limit cycle frequency and the boilerplate value of $E(t)$ increases monotonically with respect to $P$.

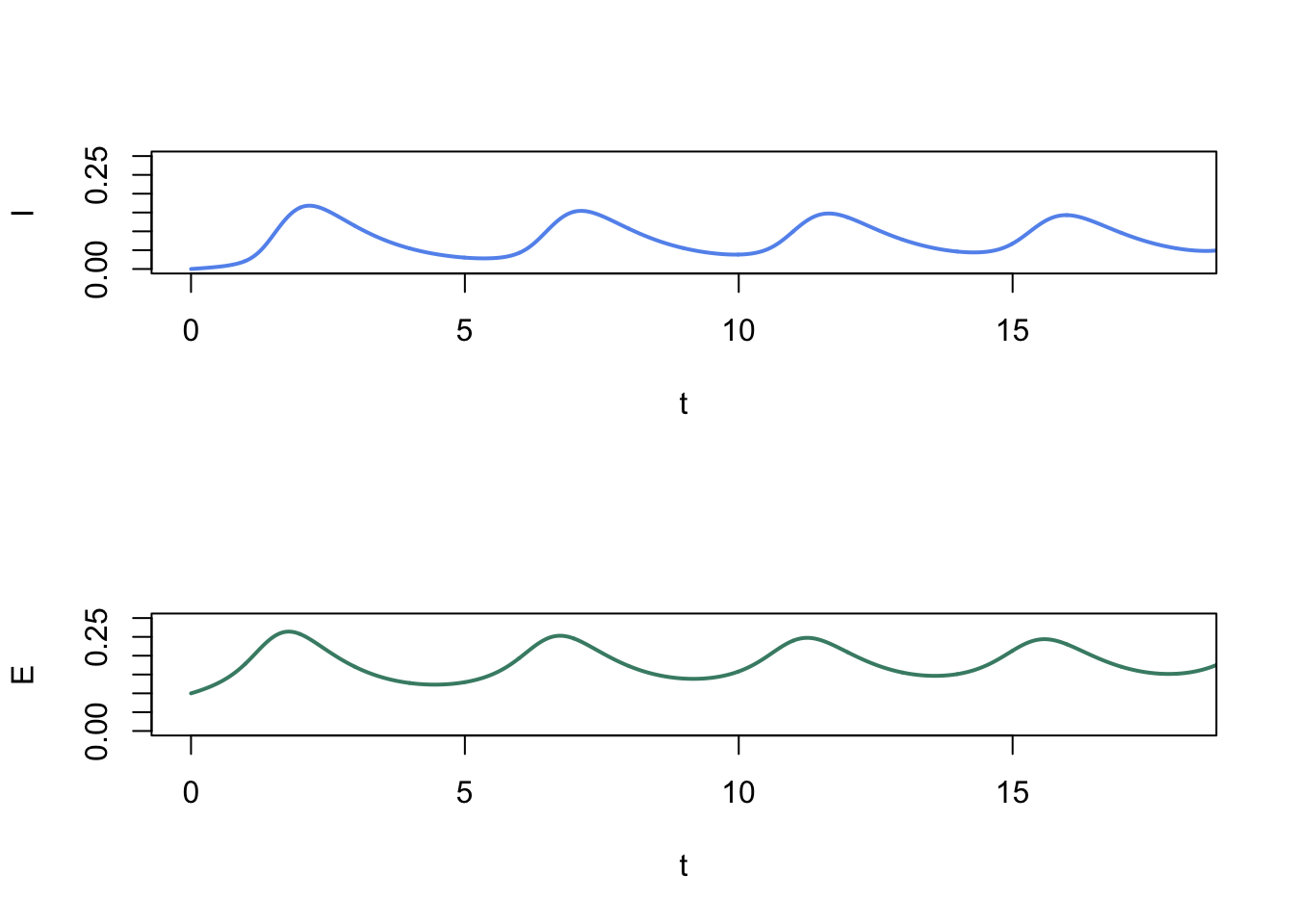
Figure 9: $I(t)$ and $E(t)$ for limit cycle shown above. The limit cycle depends on the value of $P$, i.e. $Q$ being set equal to zero.

Figure ix: $I(t)$ and $East(t)$ for limit bicycle shown above. The limit cycle depends on the value of $P$, i.e.$Q$ being fix equal to zero.

Summary

The to a higher place demonstrates the components necessary to perform qualitative analysis on a one-dimensional autonomous ODE:

plot the catamenia field
plot several trajectories one the flow field
identify the equilibrium points
cull a method to determine stability of equilibrium points

Code Appendix

            library(knitr) library(phaseR) library(deSolve) library(graphics) library(captioner) library(latex2exp) knitr::opts_chunk$set(echo = FALSE, out.width = 400, fig.marshal = "centre", message = FALSE) fig_nums <- captioner(prefix = "Figure") body_cap <- fig_nums(proper noun = "stage", caption = "Phase Portrait for $\\frac{dy}{dt}=iv-y^2$. The trajectories plotted shows that solutions converge towards $y=two$, but abroad from $y=-ii$.") example1_phasePortrait  <- phasePortrait(   example1, ylim = c(-5, 5)) body_cap2 <- fig_nums(name = "phase2", caption = "The menstruation field and various trajectories, calculation horizontal lines at equilibrium points.") example2_flowField  <- flowField(example2,                                  xlim = c(0, two),                                  ylim = c(-ane, iii),                                  system ="ane.dim",                                  add = FALSE)  grid()  example2_nullclines <- nullclines(example2,                                   xlim = c(0, 2),                                   ylim = c(-1, 3),                                   organisation = "one.dim",                                   col=c("#ff5ccd"),                                   ltw=2)  example2_trajectory <- trajectory(example2,                                   y0 = c(-0.5, 0.5, i.5, two.five),                                   tlim = c(0, iv),                                   system = "one.dim")  body_cap3 <- fig_nums(name = "phase3", caption = "The flow field and various trajectories, adding horizontal lines at equilibrium points.") example2_phasePortrait <- phasePortrait(   example2, ylim = c(-0.5, 2.v)) example2_stability_1 <- stability(   example2, ystar = 0, system = "one.dim")  example2_stability_2 <- stability(   example2, ystar = ane, system = "1.dim")  example2_stability_3 <- stability(   example2, ystar  = 2, arrangement = "one.dim") body_cap4 <- fig_nums(name = "phase4", caption = "Plot of the velocity field with several trajectories for $\\frac{dx}{dt} = 10-xy, \ \\frac{dy}{dt} = xy-y$.") lotkaVolterra_flowField    <- flowField(lotkaVolterra,                                         xlim       = c(0, 5),                                          ylim       = c(0, 5),                                         parameters = c(1, i, 1, ane),                                         add together        = F) lotkaVolterra_trajectories <- trajectory(lotkaVolterra,                                          y0     = rbind(c(ii, 2),                                                         c(0.5, 0.5),                                                         c(0.5, 1.5),                                                         c(1.five, 0.5),                                                         c(three, iii)),                                          parameters = c(1, 1, 1, 1),                                          col    = rep("blackness", five),                                          tlim   = c(0, 100)) body_cap5 <- fig_nums(proper noun = "phase5", caption = "Sketch of the nullclines for the organisation of equations $\\frac{dx}{dt} = ten-xy, \ \\frac{dy}{dt} = xy-y$.") lotkaVolterra_flowField    <- flowField(lotkaVolterra,                                         xlim       = c(-i.5,1.v),                                          ylim       = c(-1.5,one.five),                                         parameters = c(one, 1, 1, 1),                                         add together        = F) lotkaVolterra_trajectories <- nullclines(lotkaVolterra,                                          xlim      = c(-1.5,1.5),                                          ylim      = c(-i.5,1.5),                                          col = c("aquamarine2", "blueviolet"),                                          parameters = c(1, i, 1, 1),                                          points = 251) body_cap6 <- fig_nums(name = "phase6", explanation = "Plot $x$ and $y$ trajectories against $t$. In this example, nosotros can view the oscillating nature of $x$ and $y$.") lotkaVolterra_numericalSolution <- numericalSolution(lotkaVolterra,                                                      y0 = c(3, 4),                                                      tlim = c(0, fifty),                                                      parameters = c(1, 1, one, 1)) se <- function(x){   ae=1.3   theta_e=4   i/(one+exp(-ae*(x-theta_e))) }  si <- function(x){   ai=2   theta_i= three.vii   i/(1+exp(-ai*(x-theta_i))) }  WilsonCowan2 <- function(t, y, parameters) {   # couplings   c1 = xvi   c2 = 12   c3 = 15   c4 = three      # Refractory periods   rE = 1   rI = 1      # external inputs   P = ane.25   Q = 0      ki=0.825   ke=0.88   I <- y[1]   East <- y[2]   dy <- c(      -I + (ki - rI * I) * si(c3 * Due east - c4 * I + Q),      -East + (ke - rE * Due east) * se(c1 * E - c2 * I + P))   list(dy) } body_cap8 <- fig_nums(name = "phase8", caption = "Phase Plane Analysis. Determine the steady-state solution past the nullclines' intersection. Parameters: $c_1=16$, $c_2 = 12$, $c_3=15$, $c_4=three$, $a_e = 1.3$, $\\theta_e=4$, $a_i=2$, $\\theta_i = 3.vii$, $r_e=one$, $r_i=1$.") example4_flowField  <- flowField(WilsonCowan2,                                  xlim = c(-0.01, .425),                                  ylim = c(0, .5),                                  add  = FALSE,                                  ylab = TeX("$E$"),                                  xlab= TeX("$I$"),                                  frac=1) grid() example4_nullclines <- nullclines(WilsonCowan2,                                   xlim = c(-0.01, .425),                                   ylim = c(0, .five),                                   lty = 2, lwd = 2,                                   col=c("lightseagreen","aquamarine4"))  body_cap9 <- fig_nums(name = "phase9", caption = "Phase Plane Assay showing limit cycle trajectory in response to constant simulation $P=i.25$. Dashed lines are nullclines. Parameters: $c_1=xvi$, $c_2 = 12$, $c_3=xv$, $c_4=3$, $a_e = ane.3$, $\\theta_e=4$, $a_i=2$, $\\theta_i = three.seven$, $r_e=i$, $r_i=1$.") example4_flowField  <- flowField(WilsonCowan2,                                  xlim = c(-0.01, .425),                                  ylim = c(0, .5),                                  add  = Fake,                                  ylab = TeX("$E$"),                                  xlab= TeX("$I$"),                                  frac=1) grid() example4_nullclines <- nullclines(WilsonCowan2,                                   xlim = c(-0.01, .425),                                   ylim = c(0, .v),                                   lty = two, lwd = 2,                                   col=c("lightseagreen","aquamarine4"))  y0 <- matrix(c(0.1,0.3,                0,0,                0.i,0.two), 3, 2, byrow = TRUE) example4_trajectory <- trajectory(WilsonCowan2,                                   y0   = y0,                                   pch=16,                                   tlim = c(0, 100),                                   col="black",                                   add together=T, ylab=TeX("$E, I$"), xlab=TeX("$t$")) grid() body_cap10 <- fig_nums(name = "phase10", explanation = "$I(t)$ and $Due east(t)$ for limit wheel shown above. The limit cycle depends on the value of $P$, i.due east. $Q$ being set equal to zero.")  example4_solution <- numericalSolution(WilsonCowan2,                         y0 = c(0.0, 0.1),                         type = "two",                         col=c("cornflowerblue", "aquamarine4"),                         add.fable = T,                         xlab = TeX("$t$"),                         ylab = c(TeX("$I$"), TeX("$E$")),                         add together.filigree = F,                         tlim = c(0,twenty),                         lwd=2,                         ylim=c(0,0.3),                         xlim=c(0,18))

References

[1] Grayling, M. J. (2014). phaseR: An R Bundle for Phase Plane Analysis of Autonomous ODE Systems. The R Periodical 6 43–51.

davenportwainewhim.blogspot.com

Source: https://hluebbering.github.io/phase-planes/